Cálculo de Reservas: Métodos estadísticos parte 2
Entre las herramientas mas usadas por el ingeniero en el campo de la estadística se encuentra el histograma, el ajuste lineal y la generación de números pseudoaleatorios.
Histograma: es el gráfico estadístico que se utiliza para representar una serie datos continuos cuando vienen agrupados en intervalos. Sobre cada uno de estos intervalos se levanta una franja tan ancha como el intervalo y de forma que su área sea proporcional a su frecuencia. En el eje vertical se representan las frecuencias, y en el eje horizontal los valores de las variables, señalando las marcas de clase, es decir, la mitad del intervalo en el que están agrupados los datos. Normalmente se construye de forma que el área de cada franja sea igual a la correspondiente frecuencia relativa. Así el área total limitada por el histograma es igual a 1.
Ajuste lineal: Es un método estadístico que permite transformar una distribución de dos variables (una dependiente y una independiente) en una expresión analítica de la forma Y=aX+b.
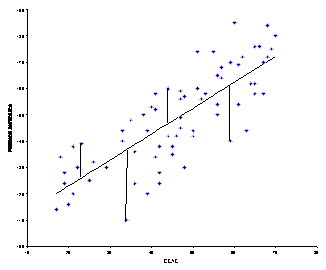
Si utilizamos un sistema de coordenadas cartesianas para representar la distribución bidimensional, obtendremos un conjunto de puntos conocido como el diagrama de dispersión, cuyo análisis permite estudiar cualitativamente, la relación entre ambas variables.
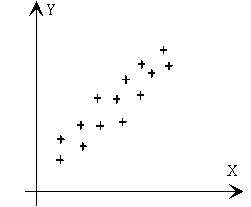Desde un punto de vista gráfico, un ajuste es la sustitución de un diagrama de dispersión por una línea, que, sin que deba pasar por todos los puntos, se adapte lo mejor posible a todos ellos, y, desde un punto de vista analítico, un ajuste es la sustitución de la dependencia de tipo estadístico existente entre dos variables por una dependencia de tipo funcional, que implica la determinación de los parámetros que caracterizan a esta función, como lo es la pendiente y el punto de corte.
La regresión nos permite además, determinar el grado de dependencia de las series de valores X e Y, prediciendo el valor y estimado que se obtendría para un valor x que no esté en la distribución.
Determinación de los parámetros:
Se denomina error ei a la diferencia yi-y, entre el valor observado yi, y el valor ajustado y= axi+b. El criterio de ajuste se toma como aquél en el que la desviación cuadrática media sea mínima, es decir, debe de ser mínima la suma.
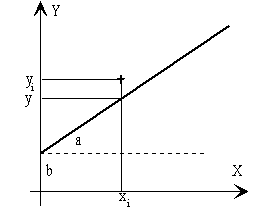
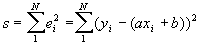
El extremo de una función, ya sea máximo o mínimo se obtiene cuando las derivadas de s respecto de a y de b sean igual a cero. Lo que genera un sistema de dos ecuaciones con dos incógnitas del que se despeja a y b.
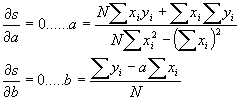El coeficiente de correlación nos indica la intensidad o grado de dependencia entre las variables X e Y. El coeficiente de correlación r es un número que se obtiene mediante la expresión:
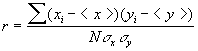El numerador es el producto de las desviaciones de los valores X e Y respecto de sus valores medios. En el denominador tenemos las desviaciones cuadráticas medias de X y de Y.
El coeficiente de correlación puede valer cualquier número comprendido en el intervalo [-1,1].
• Cuando r=1, la correlación lineal es perfecta, directa.
• Cuando r=-1, la correlación lineal es perfecta, inversa
• Cuando r=0, no existe correlación alguna, independencia total de los valores X e Y
Generación de números pseudo aleatorios:
Se llama números pseudoaleatorios a una sucesión determinística de números en el intervalo [0,1] que tiene las mismas propiedades estadísticas que una sucesión de números aleatorios. Una forma general de obtener números pseudoaleatorios es partir de una semilla de p números y aplicar una función d.
Los números pseudoaletorios son necesarios cuando se pone en práctica un modelo de simulación, para obtener observaciones aleatorias a partir de distribuciones de probabilidad.
Los números aleatorios generados en un inicio por una computadora casi siempre son números aleatorios enteros.
En sentido estricto, los números generados por una computadora no se deben llamar números aleatorios por que son predecibles y se pueden reproducir, dado el número aleatorio generador que se use. Por ello en ocasiones se les llama números pseudoaleatorios.
Lo importante es que estos números hacen las veces de números aleatorios en la simulación si el método que se usa para generarlos es válido.
El procedimiento usado por una computadora para generar números aleatorios se llama generador de números aleatorios.
La secuencia de números generados debe cumplir con las 2 hipótesis siguientes:
1) Distribución Uniforme
2) Independencia (no correlacionados)
Además son importantes los siguientes aspectos:
a) Las subsecuencias también deben cumplir 1) y 2)
b) deben ser secuencias largas y sin huecos (densas)
Los números aleatorios se pueden dividir en dos categorías principales:
° Números aleatorios enteros. Es una observación aleatoria de una distribución uniforme discretizada en el intervalo n, n+1…
Por lo general, n =0 ó 1 donde estos son valores convenientes para la mayoría de las aplicaciones.
° Números aleatorios uniformes. Es una observación aleatoria a partir de una distribución uniforme (continua) en un intervalo [a,b]
Propiedades mínimas que deberán satisfacer los números pseudoaleatorios:
*Ajustarse a una distribución U(0,1).
*Ser estadísticamente independientes (no debe deducirse un número conociendo otros ya generados).
*Ser reproducibles (la misma semilla debe dar la misma sucesión).
*Ciclo repetitivo muy largo.
*Facilidad de obtención.
Distribución uniforme
En estadística la distribución uniforme es una distribución de probabilidad cuyos valores tienen la misma probabilidad.
Distribución uniforme (caso continuo).
Se dice que una variable aleatoria X continua tiene una distribución uniforme en el intervalo [a,b] si la función de densidad de probabilidad (FDP) es
La función de distribución en el caso continuo entre a y b es
Su media estadística es
La varianza es
La distribución uniforme nos permite generar valores pseudoaleatorios entre 0 y 1.
Estos tres métodos estadísticos constituyen la base primordial de un ingeniero de yacimientos, su aplicación es extensa y forman la base de lo que hoy en día es la simulación.
Este articulo se basa en apuntes de las clases del profesor A. da Silva, y una recopilación de información en diversas paginas webs como lo es Wikipedia (conceptos basicos), y un trabajo realizado en la materia simulación del Instituto Tecnologico de Piedras Negras (generación de números pseudoaleatorios).
Histograma: es el gráfico estadístico que se utiliza para representar una serie datos continuos cuando vienen agrupados en intervalos. Sobre cada uno de estos intervalos se levanta una franja tan ancha como el intervalo y de forma que su área sea proporcional a su frecuencia. En el eje vertical se representan las frecuencias, y en el eje horizontal los valores de las variables, señalando las marcas de clase, es decir, la mitad del intervalo en el que están agrupados los datos. Normalmente se construye de forma que el área de cada franja sea igual a la correspondiente frecuencia relativa. Así el área total limitada por el histograma es igual a 1.
Ajuste lineal: Es un método estadístico que permite transformar una distribución de dos variables (una dependiente y una independiente) en una expresión analítica de la forma Y=aX+b.
Si utilizamos un sistema de coordenadas cartesianas para representar la distribución bidimensional, obtendremos un conjunto de puntos conocido como el diagrama de dispersión, cuyo análisis permite estudiar cualitativamente, la relación entre ambas variables.
Desde un punto de vista gráfico, un ajuste es la sustitución de un diagrama de dispersión por una línea, que, sin que deba pasar por todos los puntos, se adapte lo mejor posible a todos ellos, y, desde un punto de vista analítico, un ajuste es la sustitución de la dependencia de tipo estadístico existente entre dos variables por una dependencia de tipo funcional, que implica la determinación de los parámetros que caracterizan a esta función, como lo es la pendiente y el punto de corte.La regresión nos permite además, determinar el grado de dependencia de las series de valores X e Y, prediciendo el valor y estimado que se obtendría para un valor x que no esté en la distribución.
Determinación de los parámetros:
Se denomina error ei a la diferencia yi-y, entre el valor observado yi, y el valor ajustado y= axi+b. El criterio de ajuste se toma como aquél en el que la desviación cuadrática media sea mínima, es decir, debe de ser mínima la suma.
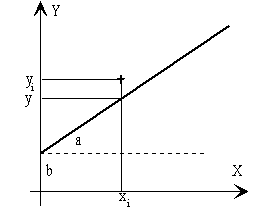
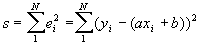
El extremo de una función, ya sea máximo o mínimo se obtiene cuando las derivadas de s respecto de a y de b sean igual a cero. Lo que genera un sistema de dos ecuaciones con dos incógnitas del que se despeja a y b.
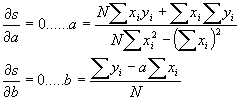El coeficiente de correlación nos indica la intensidad o grado de dependencia entre las variables X e Y. El coeficiente de correlación r es un número que se obtiene mediante la expresión: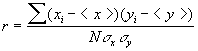El numerador es el producto de las desviaciones de los valores X e Y respecto de sus valores medios. En el denominador tenemos las desviaciones cuadráticas medias de X y de Y.El coeficiente de correlación puede valer cualquier número comprendido en el intervalo [-1,1].
• Cuando r=1, la correlación lineal es perfecta, directa.
• Cuando r=-1, la correlación lineal es perfecta, inversa
• Cuando r=0, no existe correlación alguna, independencia total de los valores X e Y
Generación de números pseudo aleatorios:Se llama números pseudoaleatorios a una sucesión determinística de números en el intervalo [0,1] que tiene las mismas propiedades estadísticas que una sucesión de números aleatorios. Una forma general de obtener números pseudoaleatorios es partir de una semilla de p números y aplicar una función d.
Los números pseudoaletorios son necesarios cuando se pone en práctica un modelo de simulación, para obtener observaciones aleatorias a partir de distribuciones de probabilidad.
Los números aleatorios generados en un inicio por una computadora casi siempre son números aleatorios enteros.
En sentido estricto, los números generados por una computadora no se deben llamar números aleatorios por que son predecibles y se pueden reproducir, dado el número aleatorio generador que se use. Por ello en ocasiones se les llama números pseudoaleatorios.
Lo importante es que estos números hacen las veces de números aleatorios en la simulación si el método que se usa para generarlos es válido.
El procedimiento usado por una computadora para generar números aleatorios se llama generador de números aleatorios.
Un generador de números aleatorios es un algoritmo que produce secuencias de números que siguen una distribución de probabilidad especifica y tienen la apariencia de aleatoriedad.
La referencia a secuencias de números aleatorios significa que el algoritmo produce muchos números aleatorios en serie.
La referencia a secuencias de números aleatorios significa que el algoritmo produce muchos números aleatorios en serie.
La secuencia de números generados debe cumplir con las 2 hipótesis siguientes:
1) Distribución Uniforme
2) Independencia (no correlacionados)
Además son importantes los siguientes aspectos:
a) Las subsecuencias también deben cumplir 1) y 2)
b) deben ser secuencias largas y sin huecos (densas)
Los números aleatorios se pueden dividir en dos categorías principales:
° Números aleatorios enteros. Es una observación aleatoria de una distribución uniforme discretizada en el intervalo n, n+1…
Por lo general, n =0 ó 1 donde estos son valores convenientes para la mayoría de las aplicaciones.
° Números aleatorios uniformes. Es una observación aleatoria a partir de una distribución uniforme (continua) en un intervalo [a,b]
Propiedades mínimas que deberán satisfacer los números pseudoaleatorios:
*Ajustarse a una distribución U(0,1).
*Ser estadísticamente independientes (no debe deducirse un número conociendo otros ya generados).
*Ser reproducibles (la misma semilla debe dar la misma sucesión).
*Ciclo repetitivo muy largo.
*Facilidad de obtención.
Distribución uniforme
En estadística la distribución uniforme es una distribución de probabilidad cuyos valores tienen la misma probabilidad.
Distribución uniforme (caso continuo).
Se dice que una variable aleatoria X continua tiene una distribución uniforme en el intervalo [a,b] si la función de densidad de probabilidad (FDP) es
La función de distribución en el caso continuo entre a y b esSu media estadística es
La varianza es
La distribución uniforme nos permite generar valores pseudoaleatorios entre 0 y 1.Estos tres métodos estadísticos constituyen la base primordial de un ingeniero de yacimientos, su aplicación es extensa y forman la base de lo que hoy en día es la simulación.
Este articulo se basa en apuntes de las clases del profesor A. da Silva, y una recopilación de información en diversas paginas webs como lo es Wikipedia (conceptos basicos), y un trabajo realizado en la materia simulación del Instituto Tecnologico de Piedras Negras (generación de números pseudoaleatorios).
