BALANCE DE MATERIALES COMO ECUACIÓN DE UNA LÍNEA RECTA

La Ley de Conservación de la materia es la base de la aplicación del Método de Balance de Materiales para análisis de yacimientos con deducciones cuantitativas y predicciones. La aplicación y la solución de esta ecuación no es difícil lo que representa una dificultad son las condiciones que se deben cumplir para obtener una solución correcta.
Estas condiciones deben ser necesarias y suficientes. Según D. Havlena y A.S.Odeh en 1963 los ingenieros tenían unas pocas condiciones necesarias pero no suficientes por ello los resultados eran inciertos aunque si se satisfacían eran aceptadas.
En general las condiciones necesarias usadas son: consistencia en los resultados no especificado y que concurran con los determinados volumetricamente. Este segundo método muchas veces se sobreestima porque los cálculos se realizan por medio de datos geológicos y petrofísicos los cuales no son muy certeros.
No se debe tomar como eficaz la afinidad de estos resultados ya que mientras el método para hallar el POES por medio de la Ec. de balance de materiales toma en cuenta el historial de presión-producción el método volumétrico se refiere al petróleo total parte del cual podría o no contribuir al historial.
Otra condición muy importante que se debe considerar necesaria con un enfoque físico y matemático que no depende de alguna interpretación geológica ó petrofísica consiste en reacomodar la ec. de balance de materiales para forma una ecuación de línea recta. Este método invalidó modelos establecidos anteriormente, no ellos era que se pensaba que existía un empuje de agua pero no se tomaba en cuenta en dicha ecuación por lo tanto el POES calculado aumentaría con el tiempo sin embargo la ecuación de balance de materiales por línea recta se demostró que no siempre era cierto.
El método de línea recta requiere la representación gráfica de diversas variables vs. otro conjunto de variables y estas dependen del mecanismo de producción que están en yacimiento. Lo prominente de este método es la secuencia de puntos trazados, la dirección que toman y la forma de la curva obtenida esto debe ser analizada para obtener un mejor resultado.
Desarrollo de la ecuación de balance de materiales para:

YACIMIENTOS SATURADOS

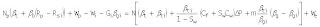Esta ecuación le llamaremos (0).
El lado izquierdo de la ec. representa la producción en barriles de yacimientos y se denota F. El otro lado (derecho) el 1er. término incluye respectivamente la expansión del petróleo Eo de la roca y el agua connota Ef,w y del gas libre, y el 2do. término representa el influjo del agua que viene dado por:

En yacimientos saturados normalmente se deprecia la expansión de la formación y agua Ef,w quedándonos la ecuación de balance de materiales así

(0.a)

Siendo ,
Si no existe alguno de estos mecanismos de producción se eliminan de la ecuación.
No hay empuje de agua ni capa de gas original la ecuación nos queda:

(1)

Siendo F=y y Eo=x podemos graficar y vs. x siendo N la pendiente de la recta.
No hay empuje de agua pero hay capa de gas:
(1.a)

Haciendo , y se grafican nos da como resultado una recta que pasa por el origen con pendiente N.

No hay empuje de agua N y m son desconocidos: La ecuación nos da dos soluciones:
(2.a)
Siendo y representa el gas de la capa de gas original en pies cúbicos y la pendiente de la recta.
Haciendo resulta una línea recta y N en este caso es la intersección con el eje y.
(2.b)
Como el m es desconocido se asumen valores de m hasta que resulte una línea recta que pase por el origen y con pendiente N.
La ecuación 2.b es mucho más precisa que la 2.a ya que debe pasar por el origen sin embargo se realizan ambas ecuaciones para equiparar.

Yacimientos con empuje de agua, dos incógnitas:

*Empuje de agua, no hay capa de gas original la ecuación nos queda:
(3.a)

Se asume una configuración de acuífero un ro/rw y un ΔtD adimensional con esto se calcula graficándose:

Si la conjetura el acuífero y el ΔtD adimensional es correcta la gráfica es una línea recta siendo el corte con el eje “y” N y C la pendiente de la recta.

Las gráficas que anteriormente se explicaron podría dar curvadas esto indicaría que los cálculos y/o datos básicos son erróneos, esto podría indicar que es muy pequeño ó muy grande.

Es especial una forma S que para su ajuste se puede asumir un influjo de agua lineal.

La secuencia de los puntos graficados de acuerdo a la ecuación 3.a se mantendrá siempre que el acuífero se comparte como un infinito, por lo que es aplicada a acuíferos infinitos o muy grandes.

En este caso, se deben emplear cálculos de influjo de agua en estado no-estable. Por otra parte, si se sospecha la presencia de un acuífero pequeño, se emplea otro caso.

Luego de que se escogen valores satisfactorios para ro/rw y ΔtD, los resultados se pueden mejorar aplicando la prueba de desviación estándar. Los valores más probables de N y C serán aquellos que correspondan al tiempo adimensional que de la misma desviación estándar (σmin).

En algunos yacimientos, la gráfica de σ vs. logΔtD no da un mínimo sino que no tiene forma definida. Este fenómeno generalmente se deriva del hecho que el yacimiento no se altere por los cambio de ΔtD. En este caso, obtener el valor de ΔtD no es necesario, sólo sería de interés académico.

Un criterio adicional empleado para evaluar los valores más probables para N y C es la prueba de consistencia, descrita a continuación. Se leen diversos valores de ΔtD cercanos al punto mínimo en la gráfica de desviación estándar. Para cada ΔtD seleccionado, se calculan N y C como funciones del tiempo, y se construyen las gráficas de N vs. el tiempo real y C Vs. el tiempo real; por medio del método de mínimos cuadrados, se traza la mejor recta a través de los puntos de cada gráfica. Seguidamente se calculan las pendientes de las rectas de C y N y se grafican vs. los correspondientes valores de ΔtD; la intersección de las 2 gráficas da el valor más probable de ΔtD. En teoría, las dos gráficas deberían interceptarse a un valor de pendiente 0 (cero). Esto se cumple porque si se eligen los ro/rw y ΔtD correctos, y si los datos de campo son certeros, entonces N y C no debería variar con el tiempo, es decir, las gráficas N-tiempo y C-tiempo deberían resultar en pendiente 0 (cero).

Un análisis estadístico nos detectaría la razón del porque la desviación de la linealidad en la obtención de la recta porque dos fuentes de errores son los procesos sistemáticos y aleatorios que se realizan para la solución de la ecuación 3.a estos métodos también nos refuerzan la consistencia de estas ecuaciones determinando un rango de incertidumbre para los valores calculados de N y C.

Se ha observado que en campos grandes el empuje de agua lineal describe satisfactoriamente el comportamiento producción-presión de dichos campos. Para un cambio de presión unitario, el influjo de agua acumulativo en un caso lineal infinito es proporcional a y no necesita determinar un tiempo adimensional y la sumatoria sería . Por esta razón se recomienda probar primero el caso infinito lineal para ver si una solución apropiada se puede obtener no obstante se debería evaluar el rango de incertidumbre para constatar los valores obtenidos de N y C.

*Acuífero muy pequeño
En este caso el influjo se puede representar:
siendo .
W’ es el volumen de agua en el acuífero y se asume una condición de agotamiento en estado estable.
La ecuación de balance de materiales se convierte en:
(3.b)
Se graficará resultando una línea recta con N como corte con el eje “y” y pendiente C’.

Se debe prestar especial atención a la represtación de los puntos deben estar ubicados a la izquierda de la gráfica ya que Eo se incrementa más rápido que ΔP’ esto ocasionaría una disminución de ΔP’/Eo a medida que baja la presión. Como la constante del influjo de agua C’ es positiva siempre entonces F/Eo también se reduce al bajar las presiones porque estas relaciones son proporcionales.
Hay que tener presente el estado estable se aprecia luego de transcurrido un tiempo en este caso los puntos se grafican hacia la derecha como en la ecuación 3.a. Sin embargo cuando se torne un estado no-estable la secuencia de puntos se revertirá ubicándose a la izquierda de la gráfica.
Una vez determinada C’ se puede calcular la cantidad del agua en acuífero.

*Empuje de agua, capa de gas conocida:

(3.c)
Una gráfica con resultaría una línea recta si se asumieron el acuífero y el tiempo adimensional correctos, En caso contrario se debe realizar el mismo procedimiento que para la ecuación 3.a.

*Acuífero muy pequeño, capa de gas conocida:
(3.d)
Esto graficado debe ser una línea recta y los puntos se grafican del lado izquierdo de la gráfica.
Hay que tener en cuenta el hecho de que cualquier valor de ro/rw y ΔtD tomado es correcto siempre y cuando satisfagan la linealidad siendo los valores muy grandes ó muy pequeños los que la curvarían y por ello se puede encontrar más de un grupo de propiedades del acuífero que contribuyan a la solución pero los valores de N y We debería ser idénticos.

*Empuje de agua, capa de gas original y N son incógnitas:

Si se deriva la ecuación 0 y el resultado se usa para eliminar m en la ecuación 0.a quedaría:
(4)
Donde siendo (´) las derivadas con respecto a la presión.

Esta ecuación al graficarla debería resultar una línea recta con corte con el eje “y” igual a N y c como pendiente una vez hallado estos valores se sustituyen en la ecuación 0 se halla el tiempo real por último se determina el valor mejor estimado de m por mínimos cuadrados.

YACIMIENTOS SUBSATURADOS

*Sin empuje de agua:

(5)

Esta ecuación al ser graficada debe resultar una línea recta que pasa por el origen, con N como pendiente siendo .

*Con empuje de agua:

(6)

Esta ecuación también debería resultar una línea recta en caso contrario hay que aplicar el procedimiento de la ecuación 3.a con yacimientos saturados.

YACIMIENTOS DE GAS

*Sin empuje de agua:
(7)

En este caso debe resultar una recta con pendiente igual a G y que pasa por el origen.

*Con empuje de agua:

(8)

Esta ecuación genera una línea recta con siendo G el corte con el eje “y” pendiente C y el procedimiento para su análisis es el mismo que la ecuación 3.a de la sección de yacimientos saturados en caso de que el acuífero sea muy grande se aplica el proceso de la ecuación 3.b.